疫情下的数学思考，疫情方程的探索与解析 疫情方程

在人类历史长河中,疫情总是伴随着人类社会的发展，从古至今，疫情的爆发不仅给人们的生命安全带来了严重威胁，也对社会经济、文化、科技等方面产生了深远的影响，面对疫情的挑战，人类需要采取各种措施来应对，而其中之一就是通过数学模型来描述和预测疫情的发展趋势，这就是我们今天要探讨的关键词——疫情方程。

疫情方程的起源与意义

疫情方程是一种数学模型,用于描述和预测疫情的发展趋势，它的起源可以追溯到上世纪，当时科学家们开始运用数学方法来研究流行病的传播规律，随着计算机技术的发展，疫情方程逐渐成为了一种重要的工具，可以帮助人们更好地了解疫情的发展趋势，制定更加科学的防控措施。

疫情方程的意义在于它能够为疫情防控提供科学依据,通过建立疫情方程，我们可以对疫情的发展趋势进行预测和分析，从而制定出更加科学、有效的防控措施，疫情方程还可以帮助我们了解疫情传播的规律和特点，为疫情防控提供更加精准的指导。

疫情方程的种类与特点

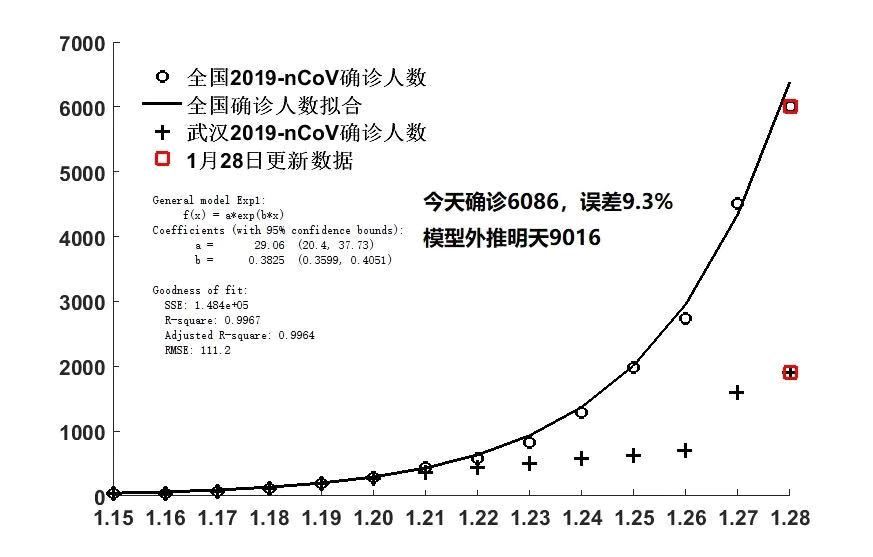
疫情方程的种类很多,根据不同的疫情传播规律和特点，可以采用不同的疫情方程进行描述和预测，最常用的疫情方程包括SEIR模型、SIR模型、SIS模型等。

SEIR模型是一种描述病毒传播过程的动态模型,它将人群分为易感者（Susceptible）、暴露者（Exposed）、感染者（Infectious）和康复者（Recovered）四个类别，通过建立SEIR模型，我们可以了解病毒在人群中的传播规律和特点，预测疫情的发展趋势。

SIR模型是一种更为简单的疫情方程,它将人群分为易感者、感染者和康复者三个类别，SIR模型可以更加直观地反映疫情的发展趋势和变化规律，是疫情防控中常用的一种模型。

SIS模型则是一种描述病毒在人群中反复传播的模型,它认为病毒可以在人群中反复传播，导致疫情的反复出现，SIS模型可以帮助我们了解病毒在人群中的传播规律和特点，为疫情防控提供更加精准的指导。

这些疫情方程的特点在于它们都是基于数学原理和计算机技术建立的动态模型,可以实时地反映疫情的发展趋势和变化规律，这些模型还可以根据不同的参数进行调整和优化，以适应不同的疫情防控需求。

疫情方程的应用与挑战

疫情方程的应用范围非常广泛,可以用于疫情防控、医疗资源调配、政策制定等方面，在疫情防控方面，疫情方程可以帮助我们了解疫情的发展趋势和变化规律，制定更加科学、有效的防控措施，在医疗资源调配方面，疫情方程可以帮助我们了解医疗资源的供需情况，合理分配医疗资源，提高医疗效率，在政策制定方面，疫情方程可以为政府提供科学依据，帮助政府制定更加科学、合理的政策。

疫情方程的应用也面临着一些挑战,疫情方程的建立需要大量的数据支持，而这些数据的获取和处理都需要耗费大量的时间和精力，疫情方程的参数调整和优化也需要专业的知识和技能，疫情方程的应用还需要考虑到不同地区、不同人群的实际情况和需求，需要进行个性化的调整和优化。

总结与展望

疫情方程是一种重要的数学工具,可以帮助我们更好地了解疫情的发展趋势和变化规律，为疫情防控提供科学依据，随着计算机技术和人工智能技术的发展，疫情方程的应用前景将更加广阔，我们可以期待更加精准、高效的疫情方程的出现，为人类的疫情防控事业提供更加有力的支持。